«La imaginación tiene el valor pragmático de adelantarse a la lenta caravana del pensamiento bien ordenado y frecuentemente reconoce la realidad antes que su pesado amo. En eso consiste su contribución esencial a una de las más extrañas colaboraciones del pensamiento: las sosegadas matemáticas y el vuelo de la imaginación.»
Matemáticas e Imaginación, Kasner y Newman
Esta frase aparece en el último párrafo del epílogo de Matemáticas e Imaginación, el libro que Edward Kasner y John Newman publicaron en 1949, donde subrayan que el vínculo entre matemáticas e imaginación es ineludible.

Paradójicamente, ochenta años después, para la mayoría de las personas de todas las edades, las matemáticas siguen habitando el rincón opuesto a la creatividad, al arte y a la libertad. No es raro que se las imagine como una antigua estatua de mármol: imponente, distante, un poco malhumorada. Una estatua que, con severos ojos inquisidores, no espera menos de nosotros que la respuesta correcta.
El libro de Kasner y Newman y el Museo Virtual de Matemáticas (MUMAT) comparten varios temas (el infinito, las geometrías, la cuarta dimensión, entre otros) y también un propósito común: transformar esta percepción, invitar a la exploración y dejarse sorprender por las matemáticas, a quien ellos llaman la reina más orgullosa del mundo intelectual.
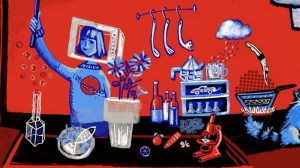
Hoy los tiempos han cambiado: en el MUMAT aprovechamos el poder de cómputo de los dispositivos electrónicos para continuar esa tarea.
Véanse en las Fig. 1(a) y 1(b) dos salas, dos experiencias: la Cabina, matemáticas para descubrir; la Cocina, matemáticas para imaginar.
En las últimas décadas hemos visto cómo disciplinas cercanas, como la astronomía, lograron despertar una fascinación colectiva indiscutible. Una generación marcada por Carl Sagan, que con sus relatos cósmicos convirtió a planetas, cometas y galaxias en habitantes habituales del imaginario común.

Cada cucharada de materia de una estrella de neutrones pesa lo que una montaña en la Tierra. Esta imagen fue generada con inteligencia artificial, a partir de esta metáfora que Carl Sagan popularizó, en los ochentas, en la serie Cosmos.
A todos nos sorprendió descubrir que una cucharadita de materia de una estrella de neutrones pesa tanto como una gran montaña. De hecho, un metro cúbico pesa aproximadamente
\(4 × 10^{17} = 400,000,000,000,000,000\ \mathrm k\mathrm g,\)
es decir, un cuatro seguido de diecisiete ceros.
Aunque este número parece enorme, se desvanece frente a \(10^{100}\) (un número que se escribe con un uno seguido de cien ceros) que el sobrino de Kasner bautizó con el nombre de gogol. Y aún más si lo comparamos con el número primo más grande conocido hasta hoy (agosto de 2025):
\(2^{136,279,841} − 1,\)
es decir, el resultado de multiplicar dos por sí mismo un poco más de 130 millones de veces y luego restar uno. Este número comienza con un 8 y continúa con más de 40 millones de dígitos. Todos esos dígitos, impresos en formato de libro, llenarían poco más de 10 mil páginas.
En el Museo Virtual de Matemáticas puedes descargar ese número (PDF). Pero date prisa: en cualquier momento podría descubrirse un primo aún mayor.

Comparado con este primo, un gogol parece casi una insignificancia; y aun así podemos imaginar infinitos números mayores. Sin embargo, de éste sabemos algo especial: es un número primo, es decir, no puede escribirse como la multiplicación de dos números más pequeños.
Esta propiedad, además de garantizarnos que los números primos son los que no aparecen en las tablas de multiplicar (salvo en la del uno, que es la más sencilla), nos permite pensarlos como los colores primarios de la aritmética.
Igual que el azul, el rojo y el amarillo pueden combinarse

para dar lugar a toda la paleta cromática, los números primos se entrelazan para generar la infinita variedad de todos los números que conocemos.
Esa es justamente la idea que inspira la Ciudad de los Números.
En la Ciudad de los Números, cada edificio es un número natural, y en ella están todos los números a partir del 2. Los números primos son edificios de un solo piso, y cada uno tiene un color único. Los edificios de dos o más pisos representan a los números compuestos: para saber qué número corresponde, basta multiplicar el valor de cada uno de sus pisos.

La Ciudad de los Números es una representación de los números naturales a partir de su descomposición en factores primos. A cada primo le corresponde un color.
La Ciudad de los Números es infinita y está llena de colores.
Puedes recorrerla a pie o, si prefieres, tomar un taxi que, por cierto, acepta operaciones matemáticas para hacer el trayecto más cómodo: sólo hay que decirle exactamente a qué número quieres llegar.
Hablemos a continuación de caleidoscopios en tres geometrías diferentes.
Un caleidoscopio es un artefacto que asombra por su sencillez y por el placer que provoca asomarse en él. Su construcción parte de tres espejos colocados en forma de prisma triangular; por eso el triángulo juega un papel fundamental. Y los triángulos, como sabemos, son figuras clásicas de la geometría plana.





 Aprovecha la cámara de tu dispositivo para hacer fotografías o pequeñas películas que puedes compartir en redes sociales.
Aprovecha la cámara de tu dispositivo para hacer fotografías o pequeñas películas que puedes compartir en redes sociales.
Cuando los espejos reflejan un triángulo, éste se repite y se acomoda como un mosaico que cubre todo el plano. Pero la geometría plana no es la única posible en dos dimensiones: también existen la geometría esférica y la hiperbólica. En cada una de ellas, los triángulos se comportan de manera distinta. En el plano, la suma de sus ángulos internos es siempre 180 grados; en la geometría esférica, esa suma es mayor; y en la hiperbólica, menor. De hecho, allí ocurren fenómenos sorprendentes: ¡hay triángulos cuya suma de ángulos internos es exactamente cero!
Cada una de estas geometrías permite construir distintos caleidoscopios. Al observar cómo los mosaicos se repiten y se distribuyen, podemos intuir la forma del espacio en el que están inscritos.
En el MUMAT puedes explorar estos caleidoscopios en las tres geometrías (plana, esférica e hiperbólica) usando la cámara de tu celular para mirar, tomar fotografías o grabar pequeños videos. Explora la app. aquí.
Seguidamente, nos referiremos al espacio de seis dimensiones de las conchas y caracolas del mar.
Imaginar cuatro dimensiones al mismo tiempo es un reto inevitable. El espacio en el que vivimos tiene tres y podemos representarlo en nuestra mente con relativa claridad. Para describir regiones dentro de él solemos recurrir a la idea de un mapa: en uno tradicional, dos coordenadas bastan para señalar un lugar preciso.
Podemos llevar esta idea más allá, aunque implica desprendernos de nuestra noción habitual de espacio. Un espacio matemático de cuatro dimensiones es aquel en el que necesito cuatro números para identificar cada punto. Lo mismo ocurre con uno de cinco, seis o diez dimensiones. Con esta perspectiva podemos asomarnos a espacios de mayor dimensión, aunque en el camino haya que sacrificar la intuición inicial que nos brinda la experiencia cotidiana.
Un ejemplo fascinante surge con las conchas y caracolas marinas. Imaginemos un espacio en el que estuvieran contenidas todas las formas posibles de estos animales. Aunque nuestra mente evoque la imagen de un mapa antiguo, pronto entendemos que dos coordenadas no bastan para describir la diversidad de cada concha o caracola.
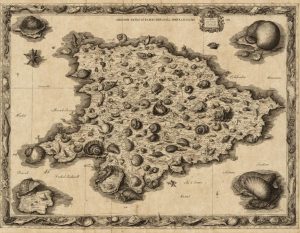
Investigaciones que combinaron matemáticas, biología y física lograron escribir una fórmula geométrica capaz de generar una sorprendente diversidad de estas formas. Con solo seis parámetros (seis números) es posible ubicar cada una dentro de ese mapa. Dicho de otro modo: el espacio de las caracolas tiene, al menos, seis dimensiones.
En el Museo Virtual puedes viajar por este extraordinario espacio de seis dimensiones mediante la app Caracoles.
Esto es apenas una muestra de lo que el MUMAT ofrece.

Recorrerlo requiere tiempo y atención, en contraste con la inmediatez que caracteriza a la mayoría de las experiencias digitales. Como parte de un reto lúdico, los visitantes son invitados a descubrir más de 150 interacciones ocultas en las ilustraciones (una especie de ¿Dónde está Wally? matemático) que solo se revelan al mirar con calma y explorar a fondo.
No todas las interacciones están disponibles desde el inicio. Como es de esperar, las historias se despliegan poco a poco, habilitando nuevas secciones y nuevos retos.

Y esto sólo después de haber recorrido las secciones anteriores. Por eso, lo mejor no es quedarse en la puerta, sino entrar hasta la cocina (ver AQUI) y recorrer sus salas en: mumat.matcuer.unam.mx.
Este es el mejor consejo que os podemos dar.
Epílogo
En la introducción de su libro, Kasner y Newman recordaban la percepción de que las matemáticas pertenecían a un pequeño grupo esotérico de eremitas, encerrados en su celda de símbolos ininteligibles. Con el MUMAT queremos romper esa imagen: mostrar que las matemáticas no son un lenguaje secreto, sino un territorio compartido, accesible a quien se atreva a mirar con calma, a explorar con curiosidad y a dejarse sorprender.

Sobre todo, queremos sembrar más matemáticas en la imaginación de la gente. Porque, al final, matemáticas, imaginación y sociedad no solo van juntas: se necesitan mutuamente.

