Esta Entrada se puede ver como una adaptación y actualización de esta otra, publicada en 2020 en el Blog del Instituto de Matemáticas de la Universidad de Sevilla.

Generalidades sobre los incendios

Con carácter general, un incendio es una aparición de fuego no controlada y no deseada. Como desgraciadamente hemos comprobado hace muy poco tiempo, los incendios pueden afectar a seres vivos y a objetos de cualquier tipo y pueden producir daños muy graves, en muchos casos irreparables.

El fuego ha estado presente en la literatura desde hace mucho tiempo, casi siempre como un agente destructivo:

– En la famosísima novela Fahrenheit 451, de Ray Bradbury, el fuego se usa para quemar libros; en la sociedad impera la idea de que el conocimiento es peligroso y dañino y la autoridad impone destrucción inmediata de todo lo que se acerca a cultura y ciencia.

– En la obra teatral Incendios, de Wajdi Mouawad, el fuego se presenta como paradigma de la violencia y la barbarie; al mismo tiempo, simboliza la miseria y calamidad que viven las personas que se ven obligadas a emigrar para salvar sus vidas.

Para una recopilación de textos, véase [1]. También ha sido parte fundamental del argumento de muchas películas. Esto ocurrió por ejemplo en Lo que el viento se llevó (1939) y, más recientemente, en Malditos bastardos (2009). Más información puede encontrarse en [2].

Los incendios pueden ser de distinto tipo, atendiendo a las propiedades físicas del combustible. Hablaremos en particular de los incendios llamados de clase A, que se caracterizan por afectar a combustibles sólidos de naturaleza orgánica: madera, tejidos, papel, etc. Y, en particular, nos referiremos a los incendios forestales.

Los incendios forestales

Para empezar, demos algunos datos que corresponden a incendios que tuvieron en su momento gran relevancia:

• En 2009 se produjo en Australia un devastador incendio. Destruyó más de 750 hogares y más de 1300 personas perdieron la vida. Tras una profunda investigación, la policía declaró que, al menos en parte, había sido provocado intencionadamente.
• En California tuvo lugar en 2020 el mayor incendio forestal de la Historia: 400.000 Ha quemadas, unas 1300 casas destruidas y un enorme daño medioambiental para la zona.
• Este verano, una buena cantidad de incendios arrasó sin piedad una buena parte de España, con resultados aterradores: A fecha de 19 de agosto alrededor de 400.000 Ha se habían quemado ya (la mitad de ellas en las provincias de Orense, León y Zamora). Así, el año 2025 se ha convertido en el peor de los últimos 30 en España. Se han señalado varias causas: el clima (extremadamente cálido), combinado con una larga sequía y vientos persistentes.

Los incendios forestales se caracterizan por su gran extensión, la velocidad con la que avanzan, los repentinos cambios de dirección y la capacidad para superar obstáculos. En ellos el fuego se suele extender sin control, afectando a todo tipo de seres vivos.

En un incendio forestal, se suelen distinguir tres fases: la iniciación (que puede deberse a causas naturales o a la acción humana), la propagación y la extinción (que también puede ser debida a causas naturales como la lluvia a la acción humana).

Casi siempre, el incendio es apagado antes de volverse fuera de control. Sin embargo, en algunos casos, la extinción es muy difícil sin cambios favorables en las condiciones atmosféricas. De hecho, hay dos maneras de «atacar» al fuego: directamente (actuando sobre el material en combustión) o con medios indirectos (preparando el terreno y las condiciones ambientales generalmente antes de la llegada del fuego; por ejemplo, improvisando cortafuegos o empapando combustibles aún no quemados).

Cómo pueden ayudar la Matemáticas a prevenir y controlar incendios

Las Matemáticas se aplican a los incendios a través de modelos que pueden ser resueltos numéricamente y predicen el comportamiento de las llamas y el humo, explican cómo se propagan e incluso indican qué hay que hacer. También se usan para desarrollar estrategias de prevención y gestión territorial y para determinar la probabilidad de que causas naturales puedan desencadenar fuegos.

Más precisamente, he aquí varias tareas concretas donde las Matemáticas pueden colaborar:

• Simulación de la propagación del fuego: Se utilizan algoritmos de dinámica de fluidos en software de simulación para recrear cómo las llamas y el humo se mueven y afectan a los objetos en un incendio real.
• Evaluación de la seguridad de edificaciones próximas: Las simulaciones permiten comprobar si la construcción de grandes edificios, como aeropuertos o estaciones, cumple con las normativas de prevención y si es viable evacuar a las personas a tiempo.
• Gestión y prevención de incendios forestales: Los modelos matemáticos ayudan a predecir el comportamiento de los incendios forestales bajo diferentes condiciones ambientales, lo que permite a los investigadores desarrollar estrategias de gestión territorial y forestal más efectivas, como la tala y limpieza de sotobosque.
• Análisis de la pirogeografía: Esta disciplina utiliza conceptos matemáticos para entender cómo interactúan los factores ambientales que facilitan la actividad del fuego, permitiendo predecir su comportamiento.
• Toma de decisiones estratégicas: Las Matemáticas son fundamentales para tomar decisiones estratégicas durante un incendio, como planificar actuaciones de los bomberos o determinar acciones preventivas.
• Análisis de la probabilidad: Se usa para calcular la probabilidad de que un incendio se deba a causas naturales, multiplicando las probabilidades de eventos individuales.

Se ha dado a conocer recientemente el trabajo de Andrea Duane, una científica de la Universidad de California (Davis). Ha realizado aportaciones notables en el contexto del modelo matemático Medfire, que permite determinar con precisión la probabilidad de que se origine un incendio, cómo será en caso de producirse y cómo puede ser combatido.

He aquí algunas afirmaciones de su autoría:

«Convierto en números todo aquello que quiero estudiar. Los números son muy importantes porque no puedes realizar una afirmación científica si no tienes unas cifras detrás que la respalden.»

«Para que se produzca un gran incendio hacen falta muchos factores, como la abundancia de vegetación, que ésta no esté húmeda … En los próximos años, todo apunta a que habrá más irregularidad en las precipitaciones y por tanto más sequías.»

Para saber más: Un modelo matemático

Para que tenga lugar un incendio, es preciso que se combinen varios elementos:

• La existencia de combustible. En lo que sigue, hablaremos de un sistema de ecuaciones dos de cuyas incógnitas son las densidades de combustible sólido y gaseoso, respectivamente denotadas \(y_s\) e \(y_g\).
• La presencia de oxígeno. Su densidad será denotada \(y_O\).
• La acción del calor que, a su vez, dependerá de los valores de la temperatura \(Q\) y de la velocidad del aire \(U\) en la región afectada por el fuego.

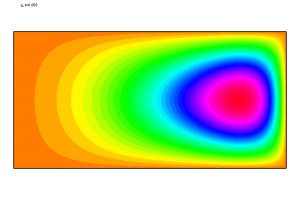
Un modelo deducido y resuelto por un grupo de investigadores de la Universidad de Salamanca [2, 3] conduce a los resultados numéricos que se muestran en las Figuras 4-6. Se trata de un sistema de ecuaciones en derivadas parciales que posee las siguientes características:

1. Se toma \(Q = q(x_1,x_2) (\delta – x_3)/(\delta – h(x_1,x_2))\), donde \(q\) es la temperatura del suelo y \(h\) es la altura o «cota» del terreno.
2. \(U = (V_1,V_2,V_3)\), con las \(V_i\) funciones de (las derivadas de) la temperatura del suelo, \(h\) y la velocidad del viento (que aquí se supone constante y de izquierda a derecha).
3. Las incógnitas resuelven un sistema no lineal de ecuaciones de evolución, con datos iniciales (en un primer instante \(t = 0\)) y de contorno (sobre el borde de la región de interés).

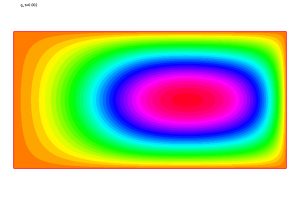
Los detalles están dados en [3, 4, 5]. Una característica importante de la ecuación satisfecha por \(q\) es la presencia de un término de la forma
\[
– \sum_{i=1}^2 \partial_i \left( \kappa_q q^3 \partial_i q \right), \ \hbox{ con } \ \kappa_q > 0 ,
\]
que indica que el calor se reparte o difunde con una intensidad proporcional al cubo de la tempreatura \(q\); esto corresponde a la llamada aproximación de Weber, véase [6].

Una manera de resolver el sistema satisfecho por estas variables en condiciones realistas y así poder determinar la evolución de un incendio (aunque sea de modo aproximado) está descrito con detalle en [3]. Esencialmente, el método consiste en aproximar en tiempo y, en cada etapa temporal, (a) calcular los valores de \(y_s\), \(y_g\), \(y_O\) y \(q\) correspondientes a valores inmediatamente anteriores; (b) actualizar los valores de las \(V_i\). De este modo, se consiguen resultados que muestran el avance de los combustibles sólido y gaseoso.

Una cuestión de enorme interés que aún no ha sido analizada en profundidad es la siguiente: ¿cómo podemos controlar este sistema desde la frontera de la zona incendiada? Es decir, ¿sobre qué datos que aparecen en las ecuaciones podríamos trabajar de manera que el fuego se reduzca en espacio y tiempo tanto como sea posible?

Referencias

1. https://osbodigital.es/2019/05/21/el-fuego-y-los-incendios-en-la-literatura/
2. https://decine21.com/peliculas/temas-de-peliculas-y-series/incendios-33
3. https://sinumcc.usal.es
4. M.I. Asensio, L. Ferragut, J. Simon, «Modelling of convective phenomena in forest fire», Rev. R. Acad. Cien. Serie A, Mat. Vol. 96 (3), 2002, pp. 299-313.
5. M.I. Asensio, L. Ferragut, «On a wildland fire model with radiation», Int. J. Numer. Meth. Engng. 2002; 54:137-157.
6. D. Bresch, J. Lemoine, J. Simon, «Nonstationary models for shallow lakes», Asympt. Anal., 22, 15-38.
7. R.O. Weber, «Towards a comprenensive wildfire spread model», Int. J. of Wildland Fire, 1 (4), 247-248.