Vito Volterra

Vito Volterra fue un matemático y físico italiano. Realizó contribuciones valiosas en Análisis Funcional, Ecuaciones Diferenciales e Integrales, Elasticidad y Biología Matemática.

Volterra fue profesor en la Scuola Normale Superiore de Pisa, en la Universidad de Turín y, a partir de 1900, en la Universidad de Roma. Fue Senador del Reino de Italia desde 1905, Presidente de la Academia Nacional y primer Presidente del Consejo Nacional de Investigaciones (CNR) desde 1923.

A la edad de 55 años, colaboró con las fuerzas aéreas italianas durante la Primera Guerra Mundial en el desarrollo de dirigibles. Propuso (y consiguió) que en ellos se usara por primera vez Helio en lugar de Hidrógeno.

En 1931 se negó a realizar el juramento de lealtad al régimen de Mussolini, por lo que fue expulsado de la universidad, del Senado, de la Academia Nacional y del CNR. Tuvo que exiliarse y pasó sus últimos años en el extranjero, aunque regresó a Roma poco antes de morir.

Lleva su nombre la ecuación integral de Volterra, una identidad que deben verificar las funciones que describen (por ejemplo) la evolución de una enfermedad donde son importantes los efectos de memoria.

Alfred Lotka

 

Alfred J. Lotka fue un matemático, químico físico y estadístico nacido en 1880 en Leópolis (entonces ciudad austro-húngara, ahora ciudad ucraniana) de padres estadounidenses.

En realidad, fue un ciudadano del mundo: realizó estudios en Birmingham (Inglaterra), Leipzig (Alemania), Cornell (EEUU) y vivió después en Nueva York. También merece la pena destacar su vena polifacética: trabajó para la General Chemical Company, la Oficina de Patentes de Estados Unidos, la Universidad Johns Hopkins y, como estadístico, para la Metropolitan Life Insurance Company.

Es conocido en bibliometría por la llamada Ley de Lotka, motivada por su deseo de medir la manera en la que personas de diferentes niveles y posibilidades contribuyen al progreso de la Ciencia. Según esta ley, fijado un tema científico, si \(A_1\) denota el número de autores que publican un artículo relevante, el número de autores que publican \(n\) artículos es aproximadamente \(A_n = A_1/n^2\).

Lotka estuvo particularmente motivado por describir el crecimiento demográfico. Una de sus aportaciones fundamentales fue la llamada ecuación de Euler-Lotka, cuyo objetivo era estimar el ritmo de crecimiento de una población a partir de una tabla de vida, donde aparecen la supervivencia y la reproducción por edad.

El modelo Lotka-Volterra

Suponemos dadas dos poblaciones en un hábitat que sólo pueden interaccionar entre sí. Supongamos que una de ellas, por su naturaleza, juega el papel de depredador, mientras que la otra constituye una presa. Pensemos en leones y gacelas, lobos y corderos, gavilanes y palomas, etc. Llamaremos \(u = u(t)\) y \(v = v(t)\) a las funciones que proporcionan en cada instante \(t\) respectivamente los números de individuos de la población depredadora y de la presa.

Queremos saber cómo evolucionan \(u\) y \(v\). Un análisis detallado muestra que, muy aproximadamente, los valores de \(u\) y de \(v\) vienen dados por la solución del sistema
\[
\left\{
\begin{array}{l} \displaystyle
\frac{du}{dt} = -a u + b uv ,
\\ \displaystyle
\frac{dv}{dt} = c v – d uv ,
\end{array}
\right.
\]
donde \(a, b, c, d\) son constantes positivas.

Aquí, \(\frac{du}{dt}\) y \(\frac{dv}{dt}\) denotan las derivadas despecto del tiempo de las funciones \(u\) y \(v\) (las velocidades con las que cambian los valores de \(u\) y \(v\). En la primera ecuación, vemos que, si fuera \(v = 0\), la población depredadora tendería a la extinción. Por el contrario, en la segunda vemos que la ausencia de depredadores permitiría a la población \(v\) crecer (y vivir en paz).

Este modelo fue propuesto inicialmente por Lotka [1] en 1925. Independientemente, fue propuesto por Volterra [2] en 1926. Curiosamente, las motivaciones de Lotka y Volterra eran distintas:

• Lotka se interesó por la evolución de lo que llamó sistemas orgánicos, tomando como ejemplo una especie de planta y un animal herbívoro.
• Volterra quería comprender la evolución de las capturas de peces en el mar Adriático, que se veían amenazados por la presencia de especies depredadoras.

El modelo de Lotka-Volterra sigue siendo la base de muchos modelos utilizados en el análisis de la dinámica de poblaciones en Ecología. La razón principal es que, a pesar de su relativa simplicidad, describe de manera acertada lo que se observa en la realidad.

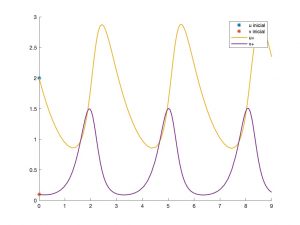
Tal vez, la característica más importante de las soluciones del sistema es que todas son periódicas en tiempo (véase la Fig. 3). Esto se puede demostrar rigurosamente y se explica con facilidad: los depredadores no pueden sobrevivir sin presas; cuando éstas empiezan a escasear, los depredadores no tienen demasiado alimento y por tanto disminuye su ritmo de crecimiento; pero entonces las presas empiezan a recuperarse y vuelven a crecer hasta valores anteriores; y así sucesivamente …

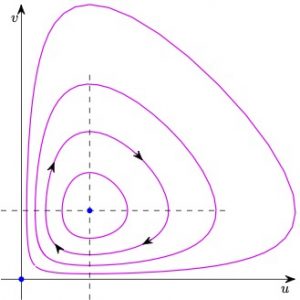
En consecuencia, en el plano de ejes \(u\) y \(v\), las curvas que describen los puntos \((u(t),v(t))\) a medida que cambia \(t\) son cíclicas (véase la Fig. 4).

Para saber más (I): Volterra y su yerno

 

Digamos más cosas de Volterra. Entre otras, que el novio de su hija (y posteriormente yerno y padre de sus nietos), Umberto D’Ancona, era biólogo marino y estaba extrañado por el inesperado crecimiento del porcentaje de tiburones en el Mediterráneo durante la Primera Guerra Mundial. D’Ancona pensaba que, al disminuir la actividad pesquera durante la guerra, tanto los tiburones como los peces de los que se alimentan aumentarían y no encontraba ninguna razón por la cual los porcentajes debían cambiar.

Conociendo la experiencia de su suegro, preguntó a éste si algún modelo matemático permitía modelar el fenómeno y explicar qué estaba ocurriendo.

Volterra triunfó en su empeño. Consideró un sistema simplificado correspondiente a sólo dos poblaciones: los tiburones (depredadores) y los peces comestibles (la presa). Supuso acertadamente que la periodicidad de las soluciones era de un año y calculó los valores medios \(\overline{u}\) y \(\overline{v}\) de ambas poblaciones. Tras un sencillo cálculo halló que
\[
\overline{u} = c/d, \quad \overline{v} = a/b .
\]

A continuación, razonó como sigue: durante la guerra, dado que se pesca menos, las especies se reproducen con mayor ritmo y en el sistema debemos cambiar el coeficiente \(a\) por \(a-\varepsilon\) y el coeficiente \(c\) por \(c+\varepsilon\). Pero esto da dos nuevos valores medios
\[
\hat{u} = (c+\varepsilon)/d, \quad \hat{v} = (a-\varepsilon)/b .
\]
Y vemos enseguida que \(\hat{u} > \overline{u}\) (hay más depredadores) y \(\hat{v} < \overline{v}\) (hay menos presas).

De este análisis, se deduce una conclusión general para un sistema de Lotka-Volterra: si las condiciones de reproducción son más favorables, se beneficia al depredador frente a la presa. Para más detalles sobre esta propiedad del sistema, véase [3].

Para saber más (II): otros modelos de poblaciones

El modelo Lotka-Volterra describe la interacción de dos especies en una situación asimétrica, cuando una de ellas juega el papel de un depredador y la otra el papel de una presa. En la Naturaleza, econtramos a veces interacciones de otro tipo:

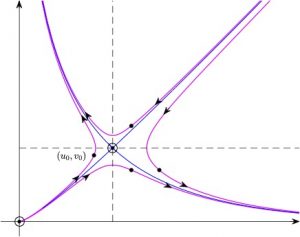
♦ Dos especies pueden competir de igual a igual por los recursos. En tal caso, su evolución puede ser modelada por las ecuaciones \(\frac{du}{dt} = a u – b uv\) y \(\frac{dv}{dt} = c v – d uv\). Lejos de ser periódicas, las soluciones del sistema muestran que, salvo en casos muy concretos (irrealizables en la práctica), una de las dos especies tiende a ser aniquilada y la otra tiende a crecer indefinidamente cuando \(t \to +\infty\). Que sea una u otra la especie dominante depende de la situación de partida (los valores de las poblaciones en un instante inicial) y de los valores de los coeficientes \(a\), \(b\), \(c\) y \(d\).; véase la Fig. 5.

♦ También puede darse el caso de co-existencia en colaboración o simbiosis. El modelo que describe esta situación es \(\frac{du}{dt} = -a u + b uv\) y \(\frac{dv}{dt} = -c u + d uv\). Ahora, pueden ocurrir tres cosas: que las dos poblaciones crezcan indefinidamente; que, a pesar de su mutua ayuda, ambas acaben extinguiéndose o que, en algún caso muy particular (y de nuevo altamente improbable en la práctica), las dos poclaciones tiendan a una situación de equilibrio. Y el comportamiento concreto depende de nuevo de las tallas de las poblaciones de partida y de los valores de los coeficientes.

Volviendo a la interacción presa-depredador, conviene indicar que existen modelos más realistas que el mencionado de Lotka-Volterra. Esto se consigue introduciendo en el sistema algunos efectos:

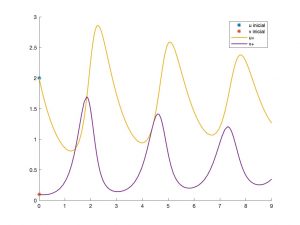
♦ Es razonable suponer que los individuos de (por ejemplo) la especie depredadora compiten entre sí por hacerse con la presa y el resto de recursos. Esto se consigue modelar cambiando la primera ecuación del sistema por la siguiente: \(\frac{du}{dt} = -a u – k u^2 + b uv\), donde \(k\) es una nueva constante positiva. Ahora la dinámica es más complicada; véase la Fig. 6.

♦ También se puede esperar un comportamiento distinto en distintas regiones geográficas, con efectos importantes. Si queremos tener en cuenta su influencia, necesitamos complicar el aparato matemático y modelar el problema con ecuaciones en derivadas parciales. Por ejemplo, un modelo presa-depredaror relativamente sencillo que determina poblaciones repartidas a lo largo de un río es el que sigue, donde \(\alpha\) y \(\beta\) son nuevas constantes positivas:
\[
\left\{
\begin{array}{l} \displaystyle
\frac{\partial u}{\partial t}
– \alpha \frac{\partial^2 u}{\partial x^2}
= -a u + b uv ,
\\  \displaystyle
\frac{\partial v}{\partial t}
– \beta \frac{\partial^2 v}{\partial x^2}
= c v – d uv ,
\end{array}
\right.
\]
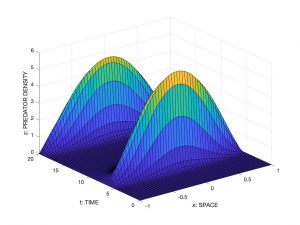
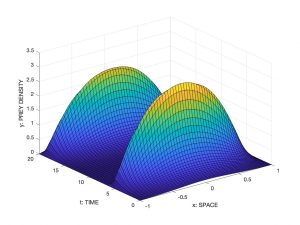
Una elección particular de los datos iniciales produce los resultados de la Fig. 7a y 7b.

♦ Finalmente, indiquemos que un tipo muy especial de interacción tiene lugar cuando se produce invasión biológica, véase [4]. El lector interesado puede encontrar detalles en la entrada «Lotka, Volterra y la Invasión Biológica», publicada en el Blog del IMUS (https://institucional.us.es/blogimus/).

Para saber más (III): algunas referencias

 

[1] A. Lotka, Elements of Physical Biology, Williams and Wilkins Company, 1925.

[2] V. Volterra, Fluctuations in the Abundance of a Species considered Mathematically, Nature volume 118, pages 558-560 (1926),

[3] M. Braun, Differential Equations and Their Applications. An Introduction to Applied Mathematics, 4th Edition, Sprnger, 1991.

[4] M.A. Lewis, S.V. Petrovskii and J.R. Potts, The Mathematics Behind Biological Invasions, Springer, 2016.